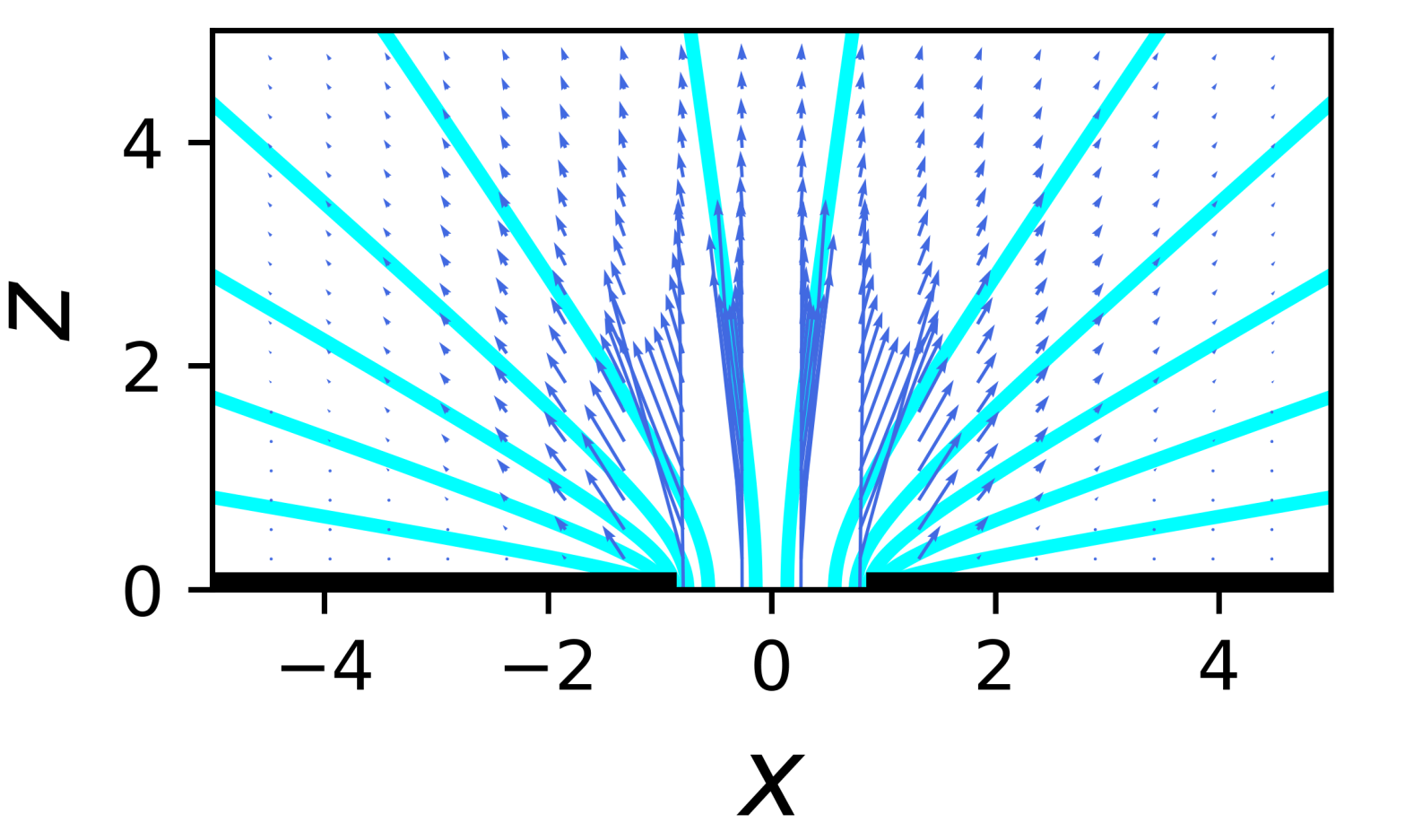
When fluids, such as air and water, flow slowly and in small systems, the equations that govern the flow simplify and become the Stokes equations. These are linear and so in simple geometries can be solved analytically, with pencil and paper. And so even before the advent of computers, a number of solutions were obtained. One of them was for flow through a circular hole in a (thin) plate. This was solved in 1891 by one Ralph Allen Sampson. The paper is a bit of a horror story of fancy maths* (in it he did many other things other than the flow through the hole) but unless I am mistaken* his result for the flow through the hole was amazingly elegant and simple, at least when viewed the right way.
The result is that the streamlines of the flow – curves that the flow follows – are simply hyperbolas, with a focal point at the edge of hole. These are shown in cyan above, with the arrows showing the flow direction on a grid of points. A hyberbola with a focus at x = ± 1 and z = 0 can be defined by the equation
where a (< 1) is a parameter that is varied as a whole family of hyperbola have a focus at x = ±1 and z = 0, and a is varied to produce the different members of this family. a is the position of what is called the vertex of the hyperbola, which is just the position of the parabola when z = 0. The parabolas, rather confusingly, have a centre at x = 0, then a vertex at x = ±a, and a focus at x = ±1, all at z = 0. Note that this equation works for both a focus at x = +1 and x =−1. Six members of this family are shown above (in cyan) for each of these two foci, and each is simply a hyperbola.
This is a beautiful result, that a fluid flowing through a hole simply follows a simple geometric curve, a hyperbola. And quite useful, since Sampson derived it the late 19th century, technology has moved forward a lot and we can now make very small holes very easily and want to flow all sorts of solutions through them. We also now know that all living cells have membranes with many pores in them, so Sampson’s elegant work helps us understand how our cells and the cells of other living things function.
* I actually took the solution from the first section of a much later paper by AMJ Davis, so thanks to them for the help following Sampson’s maths. Also, as an aside, I did not realise that the quote I have hacked for the title is due to Shakespeare (Twelfth Night).