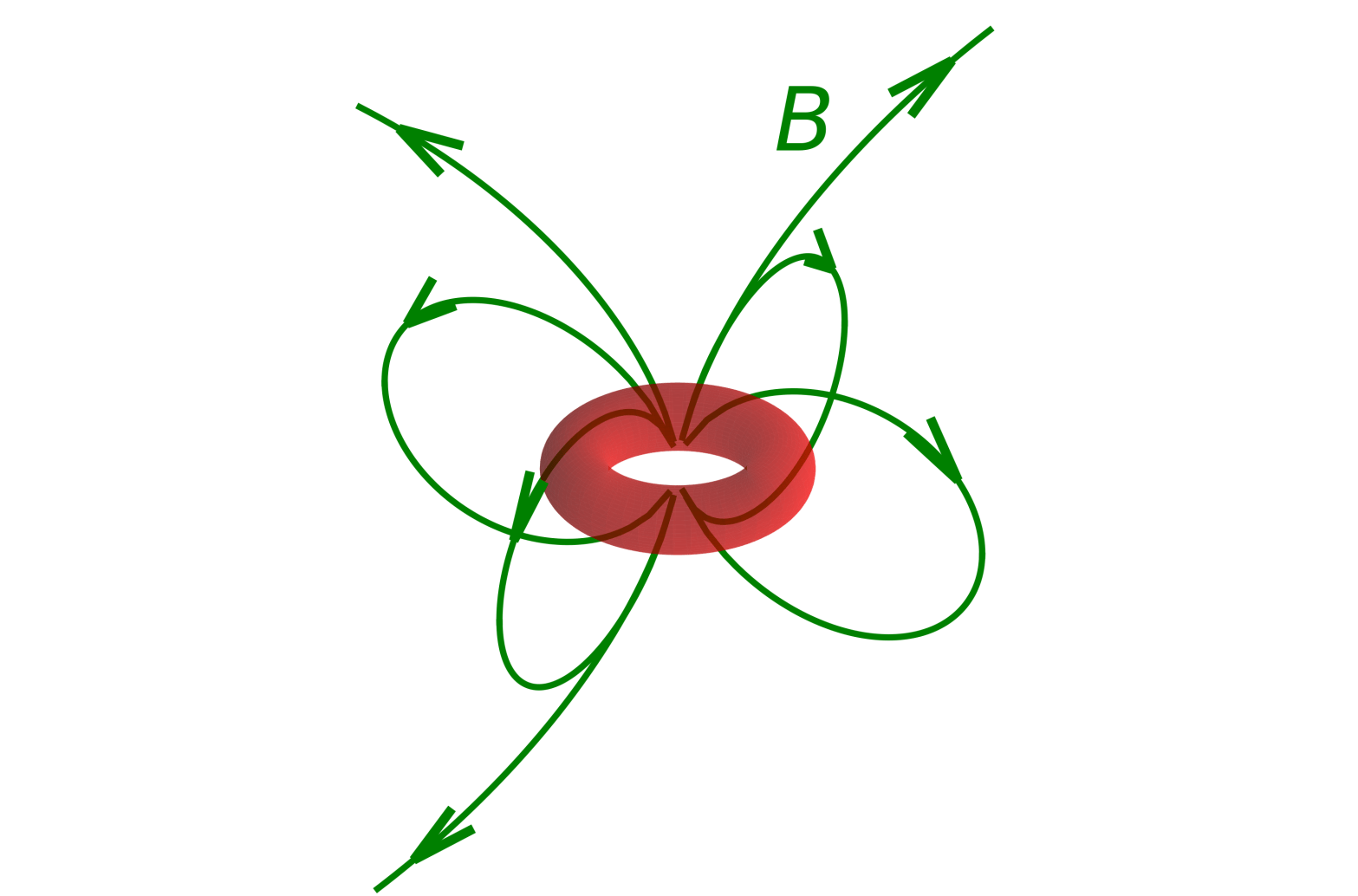
Summer at university is quieter so there is more time for doing time consuming but fun things like doing some nice figures. I like doing pretty figures but it can take more time than I have in term time. This is especially true of 3D figures that always take a lot of fiddling with details until they look OK. The image above is of the magnetic field B (green field lines and arrows) produced by a magnetic dipole*, which can be produced by the current loop shown as the red donut.
I am not 100% happy with it, but it’s OK (Colab notebook to make it is here – note that it is link to live notebook so will evolve ….). I am hoping that as the field lines that follow the magnetic field lines are computed numerically, that if I want to plot field lines (for fluid flow usually called streamlines) for another vector field I can just edit this Colab notebook by plugging in a new function and it will only take a small amount of fiddling to look OK.
As well as making me happy by being aesthetically pleasing, schematics can help with understanding the physics. As Gauss’s law of magnetism tells us, the divergence of the magnetic vector field B is zero everywhere. This means that magnetic field lines never start or end, they just go round in loops, or go off to infinity. This is clear from the field lines shown, four of them are loops, the two top ones are heading off out of the field of view, while the bottom one comes into the field of view and heads up.
So schematics can help you think about the fundamentals both of vector fields and of fundamental bits of physics such as the difference between magnetic fields which are bunches of loops, and electric fields, where the field lines start and end on charges, and so typically look very different from the schematic above.
* As an aside, as I was in a hurry/was lazy, I asked Google’s Gemini for a Python function for the 3D magnetic field of a dipole. The function was useful in the sense that it was nearly correct. Gemini’s answer should be here. However, it is wrong, there is a factor
m_dot_r = np.dot(m, r)
in the Python function which is not right, it should be
m_dot_r = np.dot(m, r_hat)
You can see this just from the dimensions, the term
(3 * m_dot_r * r_hat – m)
must have dimensions of the moment m, as r_hat is dimensionless then m_dot_r must have the same dimensions as m, which is true if it is the dot product of m and a unit vector but not if it is the dot product of m and the position vector – which has units of length. I guess this is a lesson to us all to always check code that Gemini or ChatGPT gives.